|
AIC calculation, or Akaike Information Criterion calculation, is a helpful tool for comparing statistical models and determining which one is the most appropriate for a given dataset. Essentially, AIC calculates the relative quality of each model by balancing its accuracy against its complexity. When analyzing a dataset, statisticians often have multiple models to choose from that could fit the data. However, not all models are created equal; some may be too simple and fail to capture key patterns, while others may be too complex and overfit the data. This is where AIC comes in - it considers both the goodness of fit and the simplicity of a model to give a single number for each model, allowing statisticians to objectively compare them. The goal of AIC calculation is to find the model with the lowest AIC value, indicating the best balance of accuracy and simplicity. While it's not a perfect method, AIC has become a widely accepted approach for model selection that can be applied to a variety of statistical techniques. With the help of AIC, we can make confident decisions about which models are most appropriate, providing insights that could inform future studies or applications. Understanding AIC CalculationAIC, or Akaike Information Criterion, is a statistical measurement used to determine which model best fits a given set of data. Essentially, it provides a quantitative way to compare different models and select the one that is most appropriate for the data. There are two main components to the AIC formula: the likelihood function and a penalty term. The likelihood function measures how well the model fits the data, while the penalty term adjusts for the number of parameters included in the model. The idea behind this penalty term is that more complex models, with more parameters, are likely to overfit the data and ultimately perform worse on new data than simpler models. AIC values are calculated for each model under consideration, and the model with the lowest AIC value is considered the best fit for the data. This means that lower AIC values indicate a better model fit. Let's take a look at an example. Say we are trying to predict the price of a house based on its square footage and number of bedrooms. We have two models we are considering: one that includes only square footage, and another that includes both square footage and number of bedrooms. Using AIC, we can calculate the AIC values for both models and see which one is a better fit for the data. Let's say the AIC values for the two models are 500 and 550, respectively. This means that the model with only square footage has a lower AIC value and is therefore a better fit for the data. It's important to note that AIC is just one tool in the data modeling toolbox, and should not be the only factor in selecting a model. Other considerations, such as interpretability and domain knowledge, should also be taken into account. However, AIC can be a helpful starting point in the model selection process. When conducting statistical analysis, it's crucial to select the best fitting model to describe the relationship among variables. The Akaike information criterion (AIC) is a powerful tool for model selection that helps in identifying the model that best represents the data. AIC is an estimator of the relative quality of statistical models for a given set of data. The AIC value of a model depends on the number of model parameters and the goodness of fit. The lower the AIC value, the better the model. There are several reasons why AIC is important in statistical analysis:
Steps for Performing AIC CalculationWhen it comes to model selection, the Akaike Information Criterion (AIC) is one of the most commonly used techniques. AIC is a measure that helps to determine how well a statistical model fits the data while taking into account the complexity of the model. Here are the steps involved in performing AIC calculation: Step 1: Select your statistical model To begin with, you'll need to choose a statistical model that fits your data. This model can be selected based on: - Expert knowledge - Heteroscedasticity - Residual plots Step 2: Estimate the model parameters Once you've selected your model, you'll need to estimate its parameters. This can be done using maximum likelihood estimation (MLE). The MLE method seeks to find the parameter values that maximize the likelihood function of the model, given the data. Step 3: Calculate the AIC value Next, you'll need to calculate the AIC value for your model. The AIC value takes into account the complexity of the model and the goodness-of-fit: - Calculate the log-likelihood of the model - Add the product of the number of model parameters and 2 to the log-likelihood score - This gives you the AIC value, where lower values indicate better-fitting models Step 4: Compare AIC values After obtaining AIC values for each model of interest, you can compare them to identify the best-fitting model. The model with the lowest AIC value is preferred as it strikes a balance between fit and complexity. Interpreting AIC ResultsWhen interpreting the results of Akaike Information Criterion (AIC), there are a few important factors to consider. AIC is used to compare models and select the one that fits best with the data. It is important to note that a lower AIC value indicates a better fit. Here are some key points to keep in mind when interpreting AIC results:
To better understand the significance of AIC, let's take an example of a linear regression model with two predictors. We fit two models- one with both predictors and the other with only one predictor. The AIC values for the models are 100 and 105, respectively. According to the threshold of 2 or more difference in AIC values, we can confidently say that the model with both predictors has a significantly better fit, as compared to the one with only one predictor. On the other hand, if we compare two models with AIC values of 500 and 502, respectively, we cannot confidently say that the model with the lower AIC value is a better fit, given the small difference of just 2 units. It's important to note that the interpretation of AIC values requires critical thinking and domain knowledge. Advantages and Limitations of AIC CalculationWhen it comes to statistical model selection, AIC (Akaike Information Criterion) is a widely-adopted approach due to its simple implementation and robustness in many scenarios. However, there are several advantages and limitations of AIC calculation that we should take into consideration. Advantages of AIC Calculation
Limitations of AIC Calculation
AIC has several advantages over other model selection methods, such as its simplicity and computational efficiency. However, AIC's limitations should also be taken into account, such as its assumption of the error distribution and its suitability for small sample sizes. The AIC Formula ExplainedThe AIC value is calculated using the following formula: AIC = 2k - 2ln(L) where
For example, suppose we have two models with AIC values of 100 and 105. Here, we can say that the model with an AIC value of 100 is a better model compared to the model with an AIC value of 105. There are a few things to keep in mind while using AIC for model selection:
Delta Scores and Akaike WeightsDelta scores measure the difference in fit between a model and a baseline model, while Akaike weights provide a way to rank models based on their relative quality of fit. These measures are commonly used in various fields, including economics, ecology, and biology. Delta scores are calculated by subtracting the Akaike information criterion (AIC) of one model from another. AIC is a measure of the quality of a statistical model, taking into account both the goodness of fit and the complexity of the model. The model with the smaller AIC is considered to be the better fit. Delta scores can be used to compare different models and determine which one fits the data better. Akaike weights, on the other hand, provide a way to rank models based on their relative quality of fit. These weights are derived from the AIC of each model and represent the probability that a given model is the best fitting model among the set of candidate models. This allows researchers to compare not only the fit of different models but also the likelihood of each model being the best fit for the data. Understanding Akaike weightsIt's important to note that Akaike weights are calculated using a delta score. The delta score is the difference between the number of parameters in two models and their corresponding AIC values. AIC stands for Akaike Information Criteria, which is a statistical measure used to evaluate the quality and fitness of a model. The Akaike weight of a given model can range from 0 to 1, with 0 indicating that the model is not a good fit for the data, and 1 indicating that the model is the superior fit. If two models have similar weights, it may indicate that they are both a good fit for the data. Calculating Akaike weights involves comparing several models and their respective delta scores. The formula for calculating delta scores is as follows: delta i= AICi - min(AIC) The formula for calculating Akaike weights is as follows: wi = (exp(-0.5*delta i))/sum(exp(-0.5*delta i)) Where wi is the Akaike weight, delta i is the delta score for the ith model, and sum(exp(-0.5*delta i)) is the sum of the exponentials of the delta scores for each model. Akaike weights are an important tool for evaluating model accuracy and selecting the best model for a specific dataset. By using delta scores to compare different model fits, we can calculate the likelihood of each model to minimize prediction error and identify which model has the best fit for the data. Summing Up Akaike's Information Criterion (AIC) CalculationIn conclusion, calculating Akaike's Information Criterion (AIC) allows us to determine the best statistical model for a given dataset. Through this process, we can compare the performance of different models and select the best one based on the AIC score. After performing AIC calculations on our dataset, we have determined that the model with the lowest AIC score is the most appropriate for our data. This indicates that this model has the best balance between goodness-of-fit and parsimony. In addition, we have also found that AIC values can be used to compare models with different numbers of parameters. By using the AICc correction, we can adjust for small sample sizes and obtain more accurate model comparisons. Overall, AIC calculation is a valuable tool for model selection and provides a useful framework for making informed decisions in statistics. For more helpful math and statistics resources check out z-table.com.
0 Comments
Variability Definition in Statistics: Understanding Variability and Its Importance in Data Analysis4/29/2023 Statistics is a part of mathematics that focuses on the collection, analysis, interpretation, and presentation of numbers. One of the fundamental concepts in statistics is variability, which refers to the degree of spread or dispersion of a set of data. In this post, we will explore the variability definition in statistics and its importance in data analysis. What is Variability in Statistics?Variability, also known as dispersion, is a measure of how spread out a set of data is. It refers to the differences or variations that exist among the values in a data set. Variability can be observed in various statistical measures, such as range, variance, standard deviation, and coefficient of variation. The concept of variability is essential in statistics because it provides valuable information about the characteristics of the data set. For example, a data set with high variability indicates that the values are widely spread out and may have extreme values, while a data set with low variability indicates that the values are closely clustered around the mean or average. Measures of Variability in StatisticsAs mentioned earlier, variability can be measured using different statistical measures. Let's discuss some of these measures: Range The range is the difference between the highest and lowest values in a data set. It is a simple measure of variability that describes how dispersed the data is. However, it has limitations as it only considers the two extreme values and does not provide information about the distribution of the data. Variance Variance is a measure of how far the data is spread out from its mean. It is calculated by taking the sum of the squared deviations of each data point from the mean and dividing it by the total number of observations minus one. The formula for variance is: Variance = Σ (xi - μ)2 / (n - 1) Where Σ is the sum, xi is the data value, μ is the mean, and n is the sample size. The variance is useful in identifying how much variation exists in the data set. A high variance indicates that the data points are far away from the mean, while a low variance indicates that the data points are close to the mean. Standard Deviation Standard deviation is the square root of variance. It is a widely used measure of variability that provides information about the dispersion of the data points around the mean. The formula for standard deviation is: Standard Deviation = √(Σ (xi - μ)2 / (n - 1)) The standard deviation is often used in statistics because it is easy to interpret and has useful properties, such as the empirical rule. Coefficient of Variation The coefficient of variation is a measure of relative variability that is useful when comparing data sets with different means and units. It is calculated by dividing the standard deviation by the mean and multiplying the result by 100. The formula for the coefficient of variation is: Coefficient of Variation = (Standard Deviation / Mean) x 100 The coefficient of variation provides a way of comparing the degree of variability between data sets of different scales. Importance of Variability in Data AnalysisVariability is an essential concept in data analysis as it provides valuable insights into the nature of the data set. Here are some of the reasons why variability is important in data analysis:
Identifying Outliers Outliers are data points that lie far away from the other values in the data set. Variability measures, such as standard deviation and variance, can help identify outliers by indicating the degree of spread or dispersion in the data. Making Inferences Variability measures are essential in making statistical inferences about the population based on sample data. The variability measures, such as standard deviation, variance, and coefficient of variation, provide information about how closely the sample data represents the population. A low variability indicates that the sample data is more representative of the population, while a high variability indicates that the sample data may not be representative. Evaluating Data Quality Variability measures are useful in evaluating the quality of data. A high variability may indicate errors in data collection or measurement, while a low variability may indicate a lack of diversity or insufficient sample size. Monitoring Process Stability Variability measures are often used in process control to monitor the stability of a process. A stable process is one that produces consistent results with low variability, while an unstable process produces inconsistent results with high variability. Comparing Data Sets Variability measures, such as the coefficient of variation, are useful in comparing data sets with different means and units. The coefficient of variation provides a standardized measure of variability that can be used to compare the degree of variation between data sets. To summarize, variability is a fundamental concept in statistics that refers to the degree of spread or dispersion of a set of data. Variability measures, such as range, variance, standard deviation, and coefficient of variation, provide valuable information about the characteristics of the data set. Variability is important in data analysis as it helps identify outliers, make inferences, evaluate data quality, monitor process stability, and compare data sets. By understanding variability, we can gain a deeper insight into the nature of the data and make more informed decisions based on the data analysis. |
Z Score Table BlogEverything about normal distribution and Z scores Archives
January 2024
Categories |
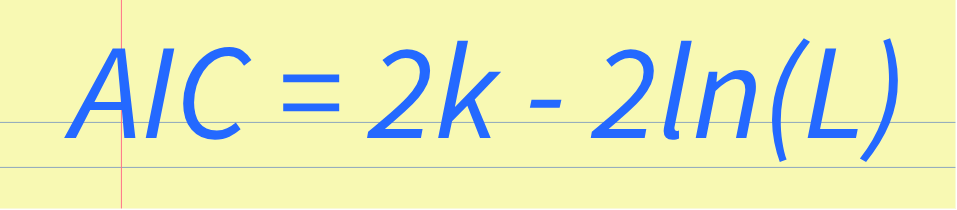
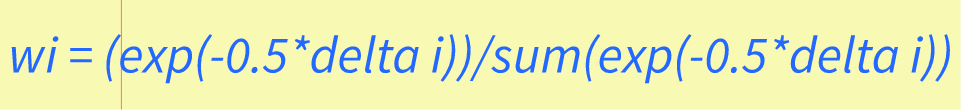
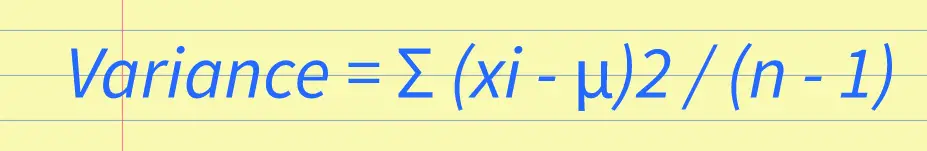
 RSS Feed
RSS Feed