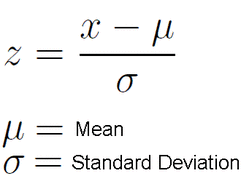How to Use the Z-Score Table

Here you can find a detailed step-by-step explanation on how you can use the z-score table (also referred as the standard normal table) to find the area (probability) corresponding to a specific z-score. 

EXAMPLE

50 randomly selected volunteers took an IQ test. Helen, one of the volunteers, scored 74 (X) from maximum possible 120 points. The average score was 62 (µ) and the standard deviation was 11 (σ). How well did she do on the test compared to other volunteers?

STEP 1: Convert to a z-score

In order to find out how well Helen did, her IQ test points need to be converted to a standardized z-score using the following formula:

In our example: (74 – 62) / 11 = 1.09090909. We can round this number to 1.09 which is the standardized score (same as z-score) that we are going to use.

STEP 2: Find the area corresponding to the z-score

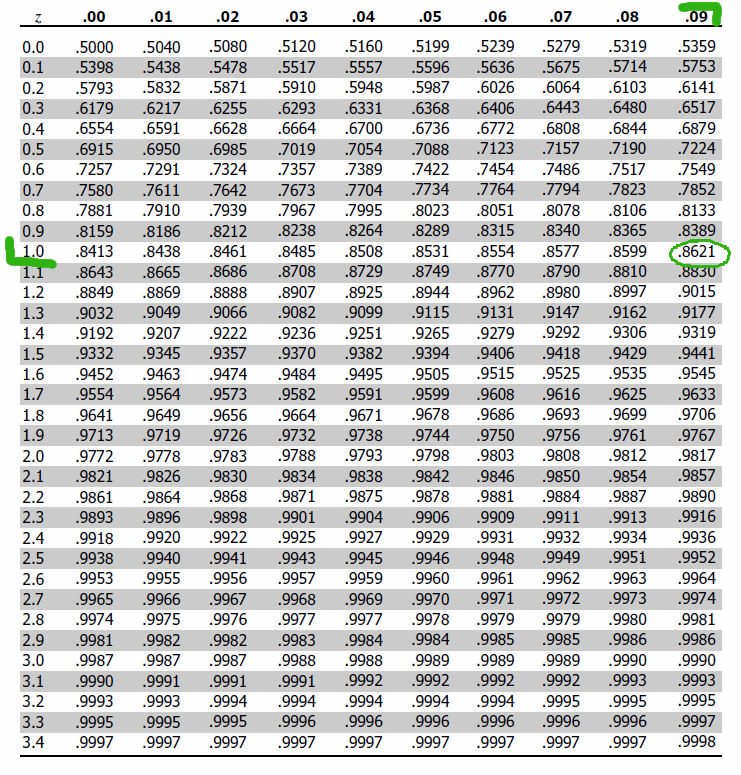
After calculating the standardized score, we need to look up the area (same as probability) using the z-table. First, we find the first two digits on the left side of the z-table. In this case it is 1.0. Then, we look up a remaining number across the table (on the top) which is 0.09 in our example. The corresponding area is 0.8621 which translates into 86.21%. On some z-tables you will find that the area corresponding to 1.09 z-score is 0.3621. Don’t be confused. Such tables just show the area to the right and the left of the mean. This means that for positive values you need to add 0.5 (i.e. 50%) to calculate the area to the left of a z-score. And indeed: 0.5 + 0.3621 = 0.8621.

STEP 3: Draw a valid conclusion

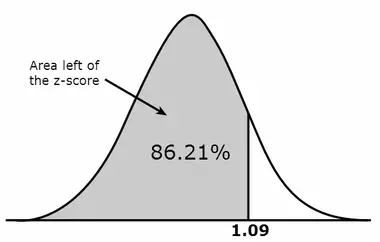
The area that we looked up in the z-table suggests that Helen received a better score than 86% of the volunteers who took the IQ test. If you would like to know an exact number of people who Helen outperformed at the test, then just multiply 50 (remember that’s how many people took the test) by 0.8621 which is 43.1. As there are no partial human beings, we just round the number to 43. Helen did better than other 43 test takers.

---