How to Calculate the Z Score: A Comprehensive Guide
In the world of statistics, it's essential to know how to compare different data points and understand how far they deviate from the average. One useful tool for this purpose is the Z score. In this comprehensive guide, we will delve into the concept of the Z score, explain why it is important, and provide a step-by-step guide on how to calculate it. By the end of this blog post, you will have a solid understanding of Z scores, their applications, and how to interpret them. If you quickly need to calculate a z score or a z score probability please check out:
Definition of Z score
The Z score, also known as the standard score, is a measure that expresses the number of standard deviations a data point is away from the mean (average) of a dataset. It is a dimensionless quantity that enables us to compare data points from different distributions or scales.
To better understand the Z score, let's break down its components:
- Standard deviation: This is a measure of the spread or dispersion of a dataset. It tells us how much the individual data points deviate from the mean, on average. The greater the standard deviation, the more dispersed the data points are from the mean.
- Mean: The mean, or average, is the sum of all data points divided by the number of data points. It represents the central value of a dataset.
For example, consider the following dataset of ages of a group of people: {20, 25, 30, 35, 40, 45, 50}. The mean age is 35, and the standard deviation is approximately 10.07. To calculate the Z score for the age of 45, we would use the formula:
Z score = (Data point - Mean) / Standard deviation
Z score = (45 - 35) / 10.07 ≈ 0.99
In this case, the Z score of 0.99 indicates that the age of 45 is approximately one standard deviation above the mean age of the group. This suggests that the age of 45 is relatively common within the dataset, as it is close to the average value.
On the other hand, if we calculate the Z score for the age of 20:
Z score = (20 - 35) / 10.07 ≈ -1.49
The negative Z score of -1.49 indicates that the age of 20 is approximately 1.5 standard deviations below the mean age of the group. This suggests that the age of 20 is less common within the dataset, as it is farther away from the average value.
Importance of Z score in statistics
Z scores are widely used in statistics because they provide a standardized way of comparing data points, regardless of the original scale. They are particularly helpful in identifying outliers, standardizing data for analysis, and comparing data from different sources.
Applications of Z score
- Comparing data from different scales: Z scores allow us to compare data points from different distributions or scales, such as test scores or financial data, by standardizing the data.
- Identifying outliers: Z scores can help determine whether a data point is an outlier, as unusually high or low Z scores suggest that the data point significantly deviates from the mean.
- Standardizing data for analysis: Z scores are often used in statistical analyses, such as regression and hypothesis testing, to ensure that the data is on a common scale.
Prerequisites for calculating Z score
Understanding the normal distribution
Familiarity with basic statistical concepts
To calculate Z scores, you need to have a basic understanding of the following statistical concepts:
- Definition and characteristics: The normal distribution, also known as the Gaussian distribution, is a continuous probability distribution characterized by its bell-shaped curve. It is symmetric around the mean, with the majority of data points concentrated near the mean and fewer data points as we move away from the mean.
- The bell curve: The bell curve is a visual representation of the normal distribution. It is called a bell curve because of its bell-like shape, with the peak corresponding to the mean, and the tails extending towards infinity in both directions.
Familiarity with basic statistical concepts
To calculate Z scores, you need to have a basic understanding of the following statistical concepts:
- Mean: The mean, or average, is the sum of all data points divided by the number of data points. It is a measure of central tendency that provides an idea of where the center of the dataset lies.
- Standard deviation: The standard deviation is a measure of the dispersion or spread of a dataset. It indicates how much the individual data points deviate from the mean on average.
- Variance: Variance is the square of the standard deviation. It represents the average of the squared differences between each data point and the mean.
Step-by-step guide to calculating Z score
To calculate the Z score, follow these steps:
Step 1: Identify the data point
First, you need to identify the data point for which you want to calculate the Z score. This data point could be a test score, a financial figure, or any other value you wish to compare with the rest of the dataset.
Step 2: Calculate the mean of the dataset
Next, calculate the mean (average) of the dataset by adding up all the data points and dividing the sum by the number of data points.
Step 3: Calculate the standard deviation of the dataset
To calculate the standard deviation of the dataset, follow these steps:
Step 4: Compute the Z score using the formula
Now that you have the mean and standard deviation, you can calculate the Z score using the following formula:
Z score = (Data point - Mean) / Standard deviation
The Z score formula expresses the distance between the data point and the mean in terms of standard deviations. A positive Z score indicates that the data point is above the mean, while a negative Z score indicates that it is below the mean. A Z score of zero means that the data point is equal to the mean.
Example with detailed calculations:
Suppose we have the following test scores for a group of students: 72, 84, 90, 66, 78, 96, and 82. We want to calculate the Z score for the test score of 90. First, we calculate the mean and standard deviation of the dataset:
Mean = (72 + 84 + 90 + 66 + 78 + 96 + 82) / 7 = 668 / 7 = 95.43 (rounded to two decimal places)
Standard deviation:
a. Subtract the mean from each data point and square the result:
(72 - 95.43)^2 = 547.90
(84 - 95.43)^2 = 131.04
(90 - 95.43)^2 = 29.58
(66 - 95.43)^2 = 863.04
(78 - 95.43)^2 = 303.80
(96 - 95.43)^2 = 0.32
(82 - 95.43)^2 = 181.04
b. Add up all the squared differences: 547.90 + 131.04 + 29.58 + 863.04 + 303.80 + 0.32 + 181.04 = 2,056.72
c. Divide the sum of squared differences by the number of data points (or by one less than the number of data points if using a sample): 2,056.72 / 7 = 293.82
d. Take the square root of the result: √293.82 = 17.14 (rounded to two decimal places)
Finally, we can calculate the Z score for the test score of 90:
Z score = (90 - 95.43) / 17.14 = -0.32 (rounded to two decimal places)
This means that the test score of 90 is 0.32 standard deviations below the mean.
Step 1: Identify the data point
First, you need to identify the data point for which you want to calculate the Z score. This data point could be a test score, a financial figure, or any other value you wish to compare with the rest of the dataset.
Step 2: Calculate the mean of the dataset
Next, calculate the mean (average) of the dataset by adding up all the data points and dividing the sum by the number of data points.
Step 3: Calculate the standard deviation of the dataset
To calculate the standard deviation of the dataset, follow these steps:
- Subtract the mean from each data point and square the result.
- Add up all the squared differences obtained in the previous step.
- Divide the sum of the squared differences by the number of data points (or by one less than the number of data points if using a sample rather than a population).
- Take the square root of the result to obtain the standard deviation.
Step 4: Compute the Z score using the formula
Now that you have the mean and standard deviation, you can calculate the Z score using the following formula:
Z score = (Data point - Mean) / Standard deviation
The Z score formula expresses the distance between the data point and the mean in terms of standard deviations. A positive Z score indicates that the data point is above the mean, while a negative Z score indicates that it is below the mean. A Z score of zero means that the data point is equal to the mean.
Example with detailed calculations:
Suppose we have the following test scores for a group of students: 72, 84, 90, 66, 78, 96, and 82. We want to calculate the Z score for the test score of 90. First, we calculate the mean and standard deviation of the dataset:
Mean = (72 + 84 + 90 + 66 + 78 + 96 + 82) / 7 = 668 / 7 = 95.43 (rounded to two decimal places)
Standard deviation:
a. Subtract the mean from each data point and square the result:
(72 - 95.43)^2 = 547.90
(84 - 95.43)^2 = 131.04
(90 - 95.43)^2 = 29.58
(66 - 95.43)^2 = 863.04
(78 - 95.43)^2 = 303.80
(96 - 95.43)^2 = 0.32
(82 - 95.43)^2 = 181.04
b. Add up all the squared differences: 547.90 + 131.04 + 29.58 + 863.04 + 303.80 + 0.32 + 181.04 = 2,056.72
c. Divide the sum of squared differences by the number of data points (or by one less than the number of data points if using a sample): 2,056.72 / 7 = 293.82
d. Take the square root of the result: √293.82 = 17.14 (rounded to two decimal places)
Finally, we can calculate the Z score for the test score of 90:
Z score = (90 - 95.43) / 17.14 = -0.32 (rounded to two decimal places)
This means that the test score of 90 is 0.32 standard deviations below the mean.
Interpretation of Z scores
What a positive, negative, or zero Z score indicates
A positive Z score indicates that the data point is above the mean, a negative Z score indicates that it is below the mean, and a zero Z score means that the data point is equal to the mean.
Z score as a measure of distance from the mean
The Z score tells us how far a data point is from the mean in terms of standard deviations. A Z score of 1, for example, indicates that the data point is one standard deviation above the mean, while a Z score of -2 indicates that it is two standard deviations below the mean.
Standard deviations and percentiles
A positive Z score indicates that the data point is above the mean, a negative Z score indicates that it is below the mean, and a zero Z score means that the data point is equal to the mean.
Z score as a measure of distance from the mean
The Z score tells us how far a data point is from the mean in terms of standard deviations. A Z score of 1, for example, indicates that the data point is one standard deviation above the mean, while a Z score of -2 indicates that it is two standard deviations below the mean.
Standard deviations and percentiles
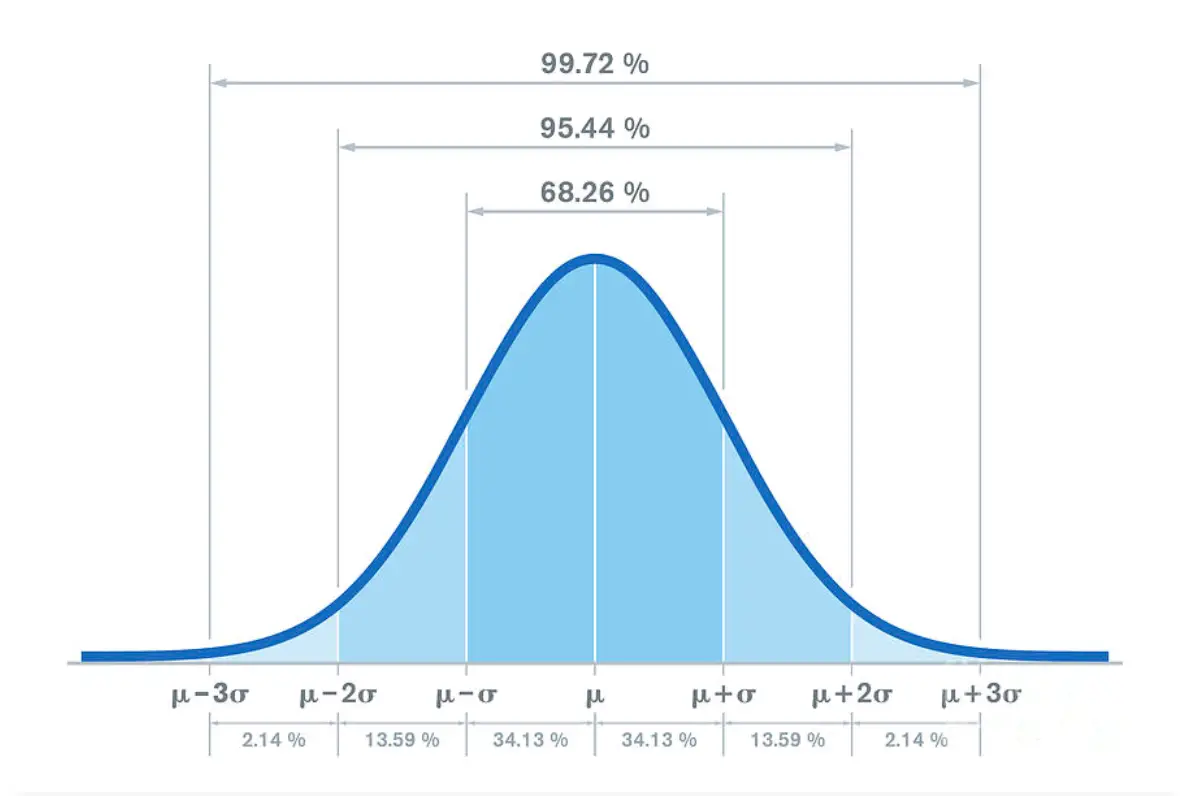
- One, two, and three standard deviation rules: In a normal distribution, approximately 68% of the data points fall within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations. These rules help us determine the probability of a data point falling within a specific range in relation to the mean.
- Using Z score to determine percentiles: The Z score can be used to find the percentile rank of a data point in a dataset. Percentile rank represents the percentage of data points that fall below a given data point. To find the percentile rank, you can use a Z score table or an online calculator that provides the area under the curve to the left of the Z score.
Applications of Z scores in real life
Comparing test scores and student performance: Z scores are often used to compare students' test scores from different schools or standardized tests, making it easier to evaluate student performance and identify areas where improvement is needed.
Financial data analysis and risk management: Z scores can help analysts and investors compare financial data from different companies, industries, or time periods, enabling them to make more informed decisions. They can also be used to assess the risk associated with investments, such as the likelihood of a stock price falling within a certain range.
Quality control in manufacturing: In manufacturing, Z scores can be used to monitor product quality and identify any deviations from the established standards. By detecting outliers, manufacturers can take corrective action to ensure that products meet the desired quality standards.
Financial data analysis and risk management: Z scores can help analysts and investors compare financial data from different companies, industries, or time periods, enabling them to make more informed decisions. They can also be used to assess the risk associated with investments, such as the likelihood of a stock price falling within a certain range.
Quality control in manufacturing: In manufacturing, Z scores can be used to monitor product quality and identify any deviations from the established standards. By detecting outliers, manufacturers can take corrective action to ensure that products meet the desired quality standards.
Limitations of Z scores
Applicability only for normally distributed data: Z scores are most accurate when the data follows a normal distribution. If the data is not normally distributed, the Z score may not accurately represent the position of a data point within the dataset.
Inaccuracy when dealing with small sample sizes: Z scores can be less accurate when dealing with small sample sizes, as the standard deviation may not be a reliable measure of dispersion.
Potential misuse in data manipulation: While Z scores can be helpful in identifying outliers and standardizing data for analysis, they can also be misused to manipulate data or draw inaccurate conclusions.
Inaccuracy when dealing with small sample sizes: Z scores can be less accurate when dealing with small sample sizes, as the standard deviation may not be a reliable measure of dispersion.
Potential misuse in data manipulation: While Z scores can be helpful in identifying outliers and standardizing data for analysis, they can also be misused to manipulate data or draw inaccurate conclusions.
How to Calculate the Z Score using a TI-89 Calculator
The TI-89 calculator is a powerful and versatile tool that can help you quickly and easily calculate Z scores. In this section, we will explain how to calculate the Z score using a TI-89 calculator, which can save you time and effort when working with statistical data.
Step-by-step guide to calculating Z score on a TI-89 calculator:
Input your dataset:
Before you can calculate a Z score on your TI-89 calculator, you need to input your dataset. Follow these steps:
a. Turn on the calculator and press the 'APPS' button. b. Scroll down the list of available applications and select '6: Data/Matrix Editor'. c. Choose '3: New' to create a new dataset. d. In the 'Type' field, select 'Data' and provide a suitable name for your dataset in the 'Var' field. Press 'Enter' to create the dataset. e. Now, input your data points into the 'c1' column. You can navigate using the arrow keys and input values by typing the numbers and pressing 'Enter'.
Calculate the mean and standard deviation:
a. Press the '2nd' button, followed by the '5' button to access the 'List' menu. b. Scroll down and select '3: mean(' and then select the dataset you created earlier by pressing '2nd', 'VAR-LINK', and choosing the dataset. Close the parenthesis and press 'Enter' to calculate the mean. c. To calculate the standard deviation, repeat the process, but select '7: stdDev(' from the 'List' menu instead. Enter the dataset name, close the parenthesis, and press 'Enter'.
Take note of the mean and standard deviation values, as you will need them to calculate the Z score.
Calculate the Z score:
To calculate the Z score for a specific data point, use the following formula:
Z score = (Data point - Mean) / Standard deviation
a. Press the 'Home' button to return to the main screen. b. Input the data point you want to calculate the Z score for, followed by the subtraction operator '-'. c. Input the mean value you calculated earlier and press 'Enter' to calculate the difference between the data point and the mean. d. Divide the result by the standard deviation value you calculated earlier, using the division operator '/'. e. Press 'Enter' to calculate the Z score for the data point.
Step-by-step guide to calculating Z score on a TI-89 calculator:
Input your dataset:
Before you can calculate a Z score on your TI-89 calculator, you need to input your dataset. Follow these steps:
a. Turn on the calculator and press the 'APPS' button. b. Scroll down the list of available applications and select '6: Data/Matrix Editor'. c. Choose '3: New' to create a new dataset. d. In the 'Type' field, select 'Data' and provide a suitable name for your dataset in the 'Var' field. Press 'Enter' to create the dataset. e. Now, input your data points into the 'c1' column. You can navigate using the arrow keys and input values by typing the numbers and pressing 'Enter'.
Calculate the mean and standard deviation:
a. Press the '2nd' button, followed by the '5' button to access the 'List' menu. b. Scroll down and select '3: mean(' and then select the dataset you created earlier by pressing '2nd', 'VAR-LINK', and choosing the dataset. Close the parenthesis and press 'Enter' to calculate the mean. c. To calculate the standard deviation, repeat the process, but select '7: stdDev(' from the 'List' menu instead. Enter the dataset name, close the parenthesis, and press 'Enter'.
Take note of the mean and standard deviation values, as you will need them to calculate the Z score.
Calculate the Z score:
To calculate the Z score for a specific data point, use the following formula:
Z score = (Data point - Mean) / Standard deviation
a. Press the 'Home' button to return to the main screen. b. Input the data point you want to calculate the Z score for, followed by the subtraction operator '-'. c. Input the mean value you calculated earlier and press 'Enter' to calculate the difference between the data point and the mean. d. Divide the result by the standard deviation value you calculated earlier, using the division operator '/'. e. Press 'Enter' to calculate the Z score for the data point.
How to Calculate a Z Score in Excel and Google Sheets
Calculating the Z score in Excel or Google Sheets is a straightforward process that can help you quickly analyze and compare data points within a dataset. We will guide you through the steps to calculate a Z score in both Excel and Google Sheets.
Step-by-step guide to calculating Z score in Excel and Google Sheets:
=AVERAGE(A1:A[n])
Replace 'A[n]' with the last cell in the range containing your dataset. Press 'Enter' to calculate the mean. For example, if your dataset ends at cell A7, the formula would be:
=AVERAGE(A1:A7)
=STDEV.S(A1:A[n]) (Excel) or =STDEV(A1:A[n]) (Google Sheets)
Replace 'A[n]' with the last cell in the range containing your dataset, and press 'Enter' to calculate the standard deviation.
Z score = (Data point - Mean) / Standard deviation
In an empty cell adjacent to the data point you want to calculate the Z score for, type the following formula:
=(A1 - Mean_Cell) / Stdev_Cell
Replace 'A1' with the cell containing the data point, 'Mean_Cell' with the cell containing the mean value, and 'Stdev_Cell' with the cell containing the standard deviation value. Press 'Enter' to calculate the Z score for the data point.
=(A1 - $B$1) / $B$2
Now you have successfully calculated the Z score for your data points using Excel or Google Sheets!
Bottom of Form
Step-by-step guide to calculating Z score in Excel and Google Sheets:
- Input your dataset:
- Calculate the mean:
=AVERAGE(A1:A[n])
Replace 'A[n]' with the last cell in the range containing your dataset. Press 'Enter' to calculate the mean. For example, if your dataset ends at cell A7, the formula would be:
=AVERAGE(A1:A7)
- Calculate the standard deviation:
=STDEV.S(A1:A[n]) (Excel) or =STDEV(A1:A[n]) (Google Sheets)
Replace 'A[n]' with the last cell in the range containing your dataset, and press 'Enter' to calculate the standard deviation.
- Calculate the Z score:
Z score = (Data point - Mean) / Standard deviation
In an empty cell adjacent to the data point you want to calculate the Z score for, type the following formula:
=(A1 - Mean_Cell) / Stdev_Cell
Replace 'A1' with the cell containing the data point, 'Mean_Cell' with the cell containing the mean value, and 'Stdev_Cell' with the cell containing the standard deviation value. Press 'Enter' to calculate the Z score for the data point.
- Calculate Z scores for all data points (optional):
=(A1 - $B$1) / $B$2
Now you have successfully calculated the Z score for your data points using Excel or Google Sheets!
Bottom of Form
How to Calculate a Z Score in R and Python
Calculating the Z score in R and Python is an essential skill for anyone working with statistical data in these popular programming languages. Here we will guide you through the steps to calculate a Z score in both R and Python.
Calculating Z Score in R:
RCopy code
data <- c(20, 25, 30, 35, 40, 45, 50)
RCopy code
mean_data <- mean(data) sd_data <- sd(data)
Z score = (Data point - Mean) / Standard deviation
For example, to calculate the Z score for the data point 45, use the following code:
RCopy code
data_point <- 45 z_score <- (data_point - mean_data) / sd_data
Calculating Z Score in Python:
pythonCopy code
import numpy as np
pythonCopy code
data = np.array([20, 25, 30, 35, 40, 45, 50])
pythonCopy code
mean_data = np.mean(data) sd_data = np.std(data)
Z score = (Data point - Mean) / Standard deviation
For example, to calculate the Z score for the data point 45, use the following code:
pythonCopy code
data_point = 45 z_score = (data_point - mean_data) / sd_data
Calculating Z Score in R:
- Input your dataset:
RCopy code
data <- c(20, 25, 30, 35, 40, 45, 50)
- Calculate the mean and standard deviation:
RCopy code
mean_data <- mean(data) sd_data <- sd(data)
- Calculate the Z score:
Z score = (Data point - Mean) / Standard deviation
For example, to calculate the Z score for the data point 45, use the following code:
RCopy code
data_point <- 45 z_score <- (data_point - mean_data) / sd_data
Calculating Z Score in Python:
- Import the required libraries:
pythonCopy code
import numpy as np
- Input your dataset:
pythonCopy code
data = np.array([20, 25, 30, 35, 40, 45, 50])
- Calculate the mean and standard deviation:
pythonCopy code
mean_data = np.mean(data) sd_data = np.std(data)
- Calculate the Z score:
Z score = (Data point - Mean) / Standard deviation
For example, to calculate the Z score for the data point 45, use the following code:
pythonCopy code
data_point = 45 z_score = (data_point - mean_data) / sd_data
Z Score Calculation Examples
Example 1:
Problem:
A teacher gives a math test to her students, and the scores are as follows: {55, 65, 75, 85, 95}. Calculate the Z score for a student who scored 75 on the test.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (55 + 65 + 75 + 85 + 95) / 5 = 375 / 5 = 75 Standard deviation = √[((55-75)^2 + (65-75)^2 + (75-75)^2 + (85-75)^2 + (95-75)^2) / 5] ≈ 14.14
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (75 - 75) / 14.14 ≈ 0
Answer: The Z score for a student who scored 75 on the test is 0. This means that the student's score is exactly at the mean of the dataset.
Explanation: The Z score of 0 indicates that the student's score is not deviating from the mean. Since the mean is the central value of the dataset, this suggests that the student's score is relatively common within the dataset.
Example 2:
Problem:
A company measures the time (in minutes) that its employees take to complete a specific task: {15, 20, 22, 24, 30}. Calculate the Z score for an employee who took 15 minutes to complete the task.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (15 + 20 + 22 + 24 + 30) / 5 = 111 / 5 = 22.2 Standard deviation = √[((15-22.2)^2 + (20-22.2)^2 + (22-22.2)^2 + (24-22.2)^2 + (30-22.2)^2) / 5] ≈ 5.09
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (15 - 22.2) / 5.09 ≈ -1.42
Answer: The Z score for an employee who took 15 minutes to complete the task is approximately -1.42.
Explanation: The negative Z score of -1.42 indicates that the employee's completion time is approximately 1.42 standard deviations below the mean completion time. This suggests that the employee's completion time is relatively fast compared to the other employees in the dataset.
Example 3:
Problem:
The weights (in kilograms) of a group of people are as follows: {60, 65, 70, 75, 80}. Calculate the Z score for a person who weighs 80 kg.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (60 + 65 + 70 + 75 + 80) / 5 = 350 / 5 = 70 Standard deviation = √[((60-70)^2 + (65-70)^2 + (70-70)^2 + (75-70)^2 + (80-70)^2) / 5] ≈ 7.07
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (80 - 70) / 7.07 ≈ 1.41
Answer: The Z score for a person who weighs 80 kg is approximately 1.41.
Explanation: The Z score of 1.41 indicates that the person's weight is approximately 1.41 standard deviations above the mean weight of the dataset. This suggests that the person's weight is relatively high compared to the other individuals in the dataset.
Example 4:
Problem:
A dataset represents the ages of a group of people: {25, 30, 35, 40, 45}. Calculate the Z score for a person who is 25 years old.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (25 + 30 + 35 + 40 + 45) / 5 = 175 / 5 = 35 Standard deviation = √[((25-35)^2 + (30-35)^2 + (35-35)^2 + (40-35)^2 + (45-35)^2) / 5] ≈ 7.07
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (25 - 35) / 7.07 ≈ -1.41
Answer: The Z score for a person who is 25 years old is approximately -1.41.
Explanation: The negative Z score of -1.41 indicates that the person's age is approximately 1.41 standard deviations below the mean age of the dataset. This suggests that the person's age is relatively low compared to the other individuals in the dataset.
By calculating Z scores for specific data points, you can easily compare and analyze values within a dataset. This statistical measure can be a helpful tool in various fields, including education, business, and research.
Problem:
A teacher gives a math test to her students, and the scores are as follows: {55, 65, 75, 85, 95}. Calculate the Z score for a student who scored 75 on the test.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (55 + 65 + 75 + 85 + 95) / 5 = 375 / 5 = 75 Standard deviation = √[((55-75)^2 + (65-75)^2 + (75-75)^2 + (85-75)^2 + (95-75)^2) / 5] ≈ 14.14
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (75 - 75) / 14.14 ≈ 0
Answer: The Z score for a student who scored 75 on the test is 0. This means that the student's score is exactly at the mean of the dataset.
Explanation: The Z score of 0 indicates that the student's score is not deviating from the mean. Since the mean is the central value of the dataset, this suggests that the student's score is relatively common within the dataset.
Example 2:
Problem:
A company measures the time (in minutes) that its employees take to complete a specific task: {15, 20, 22, 24, 30}. Calculate the Z score for an employee who took 15 minutes to complete the task.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (15 + 20 + 22 + 24 + 30) / 5 = 111 / 5 = 22.2 Standard deviation = √[((15-22.2)^2 + (20-22.2)^2 + (22-22.2)^2 + (24-22.2)^2 + (30-22.2)^2) / 5] ≈ 5.09
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (15 - 22.2) / 5.09 ≈ -1.42
Answer: The Z score for an employee who took 15 minutes to complete the task is approximately -1.42.
Explanation: The negative Z score of -1.42 indicates that the employee's completion time is approximately 1.42 standard deviations below the mean completion time. This suggests that the employee's completion time is relatively fast compared to the other employees in the dataset.
Example 3:
Problem:
The weights (in kilograms) of a group of people are as follows: {60, 65, 70, 75, 80}. Calculate the Z score for a person who weighs 80 kg.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (60 + 65 + 70 + 75 + 80) / 5 = 350 / 5 = 70 Standard deviation = √[((60-70)^2 + (65-70)^2 + (70-70)^2 + (75-70)^2 + (80-70)^2) / 5] ≈ 7.07
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (80 - 70) / 7.07 ≈ 1.41
Answer: The Z score for a person who weighs 80 kg is approximately 1.41.
Explanation: The Z score of 1.41 indicates that the person's weight is approximately 1.41 standard deviations above the mean weight of the dataset. This suggests that the person's weight is relatively high compared to the other individuals in the dataset.
Example 4:
Problem:
A dataset represents the ages of a group of people: {25, 30, 35, 40, 45}. Calculate the Z score for a person who is 25 years old.
Solution:
Step 1: Calculate the mean and standard deviation.
Mean = (25 + 30 + 35 + 40 + 45) / 5 = 175 / 5 = 35 Standard deviation = √[((25-35)^2 + (30-35)^2 + (35-35)^2 + (40-35)^2 + (45-35)^2) / 5] ≈ 7.07
Step 2: Calculate the Z score.
Z score = (Data point - Mean) / Standard deviation Z score = (25 - 35) / 7.07 ≈ -1.41
Answer: The Z score for a person who is 25 years old is approximately -1.41.
Explanation: The negative Z score of -1.41 indicates that the person's age is approximately 1.41 standard deviations below the mean age of the dataset. This suggests that the person's age is relatively low compared to the other individuals in the dataset.
By calculating Z scores for specific data points, you can easily compare and analyze values within a dataset. This statistical measure can be a helpful tool in various fields, including education, business, and research.