Scale Factor
Scale factor is a vital concept in geometry and design, used to compare the dimensions of similar shapes. Learn how to calculate scale factor and its practical applications in architecture, engineering, and more. Discover how scale factor can be used to find missing measurements and introduce students to ratios and proportions. With a solid understanding of scale factor, you can ensure precision and accuracy in your work and communicate clearly with others in your field. Master this essential concept and improve your skills today.
Understanding Scale Factor
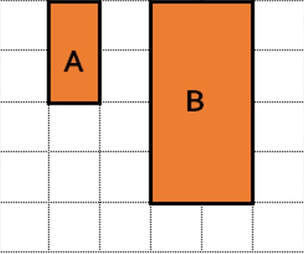
In geometry, a scale factor is a number that indicates how many times larger or smaller one geometric figure is compared to another figure. It is a crucial concept in understanding similarity and congruence of shapes. In this article, we will delve into the definition and application of scale factors, including examples and subheadings.
What is a Scale Factor?
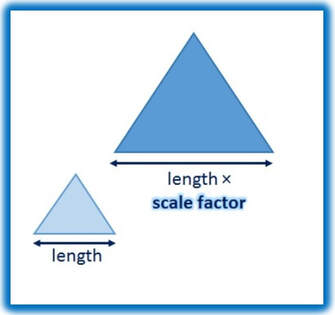
A scale factor is a numerical ratio that compares the size of two similar figures. The ratio of the corresponding lengths, widths, or heights of the figures is the scale factor. For example, if a rectangle has a length of 4 units and a width of 2 units, and a similar rectangle has a length of 8 units and a width of 4 units, the scale factor of the two rectangles is 2:1. This means that the second rectangle is twice as large as the first.
The scale factor is often expressed as a fraction or a decimal. If the scale factor is greater than 1, the second figure is an enlargement of the first. If the scale factor is less than 1, the second figure is a reduction of the first. A scale factor of 1 means the figures are congruent.
The scale factor is often expressed as a fraction or a decimal. If the scale factor is greater than 1, the second figure is an enlargement of the first. If the scale factor is less than 1, the second figure is a reduction of the first. A scale factor of 1 means the figures are congruent.
How to Find Scale Factor?
To find the scale factor of two similar figures, we need to compare their corresponding sides. We can do this by dividing the length of one side of the first figure by the corresponding length of the second figure. This process should be done for all corresponding sides, and the results should be the same.
For example, consider two similar triangles with side lengths of 6 cm and 9 cm and 8 cm and 12 cm, respectively. To find the scale factor, we divide the length of one side of the first triangle by the corresponding length of the second triangle:
6/8 = 0.75
9/12 = 0.75
Therefore, the scale factor of the two triangles is 0.75:1 or 3:4.
Another way to find the scale factor is by comparing the areas of the similar figures. If we know the ratio of the areas of the two figures, we can find the square root of the ratio to get the scale factor.
For example, consider two similar rectangles with areas of 24 square centimeters and 96 square centimeters. To find the scale factor, we divide the larger area by the smaller area:
96/24 = 4
The ratio of the areas is 4:1. To find the scale factor, we take the square root of 4, which is 2. Therefore, the scale factor of the two rectangles is 2:1.
In some cases, the scale factor may be given, and we need to use it to find missing measurements. To do this, we can multiply the known measurements by the scale factor to find the missing measurements.
For example, consider two similar triangles with a scale factor of 1:3. What is the length of the corresponding side in the larger triangle if one side of the smaller triangle measures 4 cm?
To find the length of the corresponding side in the larger triangle, we can multiply the length of the smaller triangle by the scale factor:
4 cm x 3 = 12 cm
Hence, the length of the corresponding side in the bigger triangle measures 12 cm.
For example, consider two similar triangles with side lengths of 6 cm and 9 cm and 8 cm and 12 cm, respectively. To find the scale factor, we divide the length of one side of the first triangle by the corresponding length of the second triangle:
6/8 = 0.75
9/12 = 0.75
Therefore, the scale factor of the two triangles is 0.75:1 or 3:4.
Another way to find the scale factor is by comparing the areas of the similar figures. If we know the ratio of the areas of the two figures, we can find the square root of the ratio to get the scale factor.
For example, consider two similar rectangles with areas of 24 square centimeters and 96 square centimeters. To find the scale factor, we divide the larger area by the smaller area:
96/24 = 4
The ratio of the areas is 4:1. To find the scale factor, we take the square root of 4, which is 2. Therefore, the scale factor of the two rectangles is 2:1.
In some cases, the scale factor may be given, and we need to use it to find missing measurements. To do this, we can multiply the known measurements by the scale factor to find the missing measurements.
For example, consider two similar triangles with a scale factor of 1:3. What is the length of the corresponding side in the larger triangle if one side of the smaller triangle measures 4 cm?
To find the length of the corresponding side in the larger triangle, we can multiply the length of the smaller triangle by the scale factor:
4 cm x 3 = 12 cm
Hence, the length of the corresponding side in the bigger triangle measures 12 cm.
How to Use Scale Factor?
Scale factor is a crucial concept in geometry that is used to create accurate representations of objects and structures. It can be used to determine the size of similar figures, as well as to find missing measurements in a figure. Here are some ways to use scale factor:
- Determine the size of similar figures: To determine the size of two similar figures, we can use the scale factor to compare their corresponding lengths, widths, or heights. For example, if a square has a side length of 2 cm and a similar square has a side length of 4 cm, the scale factor is 2:1. This means that the second square is twice as large as the first.
- Find missing measurements: If we know the scale factor and some of the measurements of a figure, we can use it to find missing measurements. For example, if we know that a rectangle with a length of 6 cm and a width of 3 cm is similar to another rectangle with a length of 12 cm, we can use the scale factor to find the width of the second rectangle. The scale factor is 12/6 = 2, so the width of the second rectangle is 3 cm x 2 = 6 cm.
- Compare different aspects of similar figures: We can also use scale factor to compare different aspects of similar figures. For example, if we have two similar triangles, we can compare their areas by using the square of the scale factor. If the scale factor is 2:1, the area of the larger triangle is 4 times the area of the smaller triangle.
Applications of Scale Factor
As a crucial concept in geometry, scale factor is used in many real-life applications. Some of the most common applications of scale factor include:
Maps
Maps are one of the most common uses of scale factors. A map is a representation of a larger area, and the scale factor is used to determine the ratio of the map to the actual size of the area being represented. For example, a map with a scale factor of 1:10,000 means that one unit on the map represents 10,000 units on the ground.
Models
Scale factors are also used to create models of real-life objects. Architects and engineers use scale factors to create models of buildings and bridges to show how they will look in real life. For example, a scale factor of 1:50 means that every 1 cm on the model represents 50 cm on the actual building.
Art
Artists also use scale factors to create proportional drawings and paintings. For example, a portrait artist may use a scale factor to create a larger painting of a subject by maintaining the same proportions as a smaller sketch.
Engineering
Scale factor is used in engineering to create scaled drawings of objects and structures. Engineers use scale factors to create models and blueprints of buildings, bridges, and other structures to test their design and functionality.
Photography
Scale factor is used in photography to create panoramic images. By taking multiple photos of a scene and then stitching them together, photographers can create a larger image that maintains the same proportions as the individual photos. This is done using a scale factor to ensure that the final image is proportional to the original scene.
Examples of Scale Factor
Let's take a look at some examples of scale factor:
Example 1:
The dimensions of a rectangle are 8 cm in length and 6 cm in width. If a similar rectangle has a length of 12 cm, what is its width?
To find the width of the second rectangle, we need to use the scale factor between the two rectangles. The scale factor is:
12/8 = 1.5
This means that the second rectangle is 1.5 times larger than the first rectangle. To find the width of the second rectangle, we multiply the width of the first rectangle by the scale factor:
6 x 1.5= 9 cm
As a result, the second rectangle has a width of 9 cm.
Example 2:
If a real car is 16 feet long, what would be the length of a model car that has a scale factor of 1:24?
To find the length of the model car, we need to convert the scale factor to a fraction:
1/24
Next, we need to multiply the length of the real car by the fraction:
16 x 1/24 = 0.67 feet
Thus, the model car's length measures 0.67 feet.
Example 3:
Given that the perimeter of a smaller triangle is 18 cm and the scale factor between two similar triangles is 2:3, what is the perimeter of the larger triangle?
To find the perimeter of the larger triangle, we need to use the scale factor to determine the ratio of the perimeters of the two triangles. The scale factor is:
3/2
To find the perimeter of the larger triangle, we multiply the perimeter of the smaller triangle by the scale factor:
18 x 3/2 = 27 cm
Therefore, the perimeter of the larger triangle is 27 cm.
Example 1:
The dimensions of a rectangle are 8 cm in length and 6 cm in width. If a similar rectangle has a length of 12 cm, what is its width?
To find the width of the second rectangle, we need to use the scale factor between the two rectangles. The scale factor is:
12/8 = 1.5
This means that the second rectangle is 1.5 times larger than the first rectangle. To find the width of the second rectangle, we multiply the width of the first rectangle by the scale factor:
6 x 1.5= 9 cm
As a result, the second rectangle has a width of 9 cm.
Example 2:
If a real car is 16 feet long, what would be the length of a model car that has a scale factor of 1:24?
To find the length of the model car, we need to convert the scale factor to a fraction:
1/24
Next, we need to multiply the length of the real car by the fraction:
16 x 1/24 = 0.67 feet
Thus, the model car's length measures 0.67 feet.
Example 3:
Given that the perimeter of a smaller triangle is 18 cm and the scale factor between two similar triangles is 2:3, what is the perimeter of the larger triangle?
To find the perimeter of the larger triangle, we need to use the scale factor to determine the ratio of the perimeters of the two triangles. The scale factor is:
3/2
To find the perimeter of the larger triangle, we multiply the perimeter of the smaller triangle by the scale factor:
18 x 3/2 = 27 cm
Therefore, the perimeter of the larger triangle is 27 cm.
Summary
To sum up, the concept of scale factor is crucial in geometry and has various real-life applications. Understanding the relationship between two similar figures and finding their scale factor can help solve problems in different fields, such as architecture, art, and engineering. It also plays a significant role in creating models and visual representations of real-world objects. The ability to work with scale factors is essential in developing problem-solving skills and enhancing mathematical abilities. By mastering the concept of scale factor, you can broaden your understanding of geometry and apply it to real-life situations, making it an important tool for success in various fields.
For different types of calculators and math and stats related resources visit z-table.com.