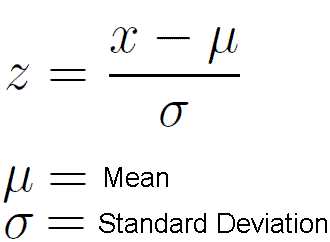Z Score Formula
This is a Z-score formula for a known mean and a standard deviation is used to calculate z score:
Here is a z score formula which can be copied and pasted:
z = (x - μ) / σ
Where:
x: the data point you want to calculate the z-score for
μ: the mean of the population or sample
σ: the standard deviation of the population or sample
x: the data point you want to calculate the z-score for
μ: the mean of the population or sample
σ: the standard deviation of the population or sample
If you need to quickly calculate a z score or would like to double check if your calculation using this formula is correct you can use this z score calculator below:
Z-score Calculator
By Z-Table.com
Now that you have calculated a z score, you likely will need to lookup corresponding probability levels in a z score table. To look up both right tail and left tail z score probabilities visit Z Table. Alternatively you can use our Z Score Probability Calculator to quickly calculate left tail and right tail probabilities. You can also scroll down to find this calculator.
About Z Score Formula
Z-score is a widely used standardized score in statistics. It is used when the population parameters (mean and standard deviation) are known. When the population parameters are unknown and only those of samples are known the Student’s t-statistic is used. Z-score derives its name from the normal distribution which is also known as the “z distribution” in statistics. A positive z-value indicates a standard score which is above the mean, while a negative corresponds to a below the mean score.
It is a very useful statistic for calculating the probability of a value occurring within a normal distribution. Z-score also allows a comparison of two scores which come from different normal distributions. This is achieved by converting raw to standardized scores.
Z Score Formula Application Example
The z-score is a way of standardizing a data point based on its distance from the mean of the population or sample. It tells you how many standard deviations away from the mean a particular data point is.
For example, suppose you have a sample of test scores for a class of students, and the mean score is 75 with a standard deviation of 10. If a student scored 85 on the test, you can calculate their z-score as follows:
z = (85 - 75) / 10 = 1
This means that the student's score is one standard deviation above the mean score for the class.
The z-score is an important concept in statistics because it allows you to compare data points from different populations or samples on a common scale. It also helps you identify outliers and extreme values in your data set.
For example, suppose you have two data sets with different means and standard deviations. Without standardizing the data, it would be difficult to compare the two sets directly. However, by calculating the z-scores for each data point, you can compare them on a common scale and make meaningful comparisons. Let's no look at an example to illustrate how z-scores can be used to compare two data sets with different means and standard deviations.
Imagine we need to compare the heights of Group A and Group B. Group A consists of 50 men with a mean height of 70 inches and a standard deviation of 3 inches. Group B consists of 50 women with a mean height of 64 inches and a standard deviation of 2.5 inches.
If you were to compare the raw data without standardizing it, it would be difficult to draw any meaningful conclusions. The heights of the men in Group A would be much higher than the heights of the women in Group B, simply because men are typically taller than women. However, by calculating the z-scores for each data point, you can compare the heights on a common scale and make meaningful comparisons.
To calculate the z-score for each data point, you would use the formula:
z = (x - μ) / σ
For Group A, the z-score for each data point would be:
z = (x - 70) / 3
For example, if a man in Group A is 73 inches tall, his z-score would be:
z = (73 - 70) / 3 = 1
For Group B, the z-score for each data point would be:
z = (x - 64) / 2.5
For example, if a woman in Group B is 66 inches tall, her z-score would be:
z = (66 - 64) / 2.5 = 0.8
By calculating the z-scores for each data point, you can compare the heights of the two groups on a common scale. A z-score of 1 in Group A represents a height that is one standard deviation above the mean for that group, while a z-score of 0.8 in Group B represents a height that is 0.8 standard deviations above the mean for that group.
You can also compare the distributions of the two groups by looking at the z-score distributions. The z-score distribution for Group A would have a mean of 0 and a standard deviation of 1, while the z-score distribution for Group B would have a mean of 0 and a standard deviation of 1. In other words, the z-scores for both groups are on the same scale and can be compared directly.
By comparing the z-scores for each data point and the z-score distributions of the two groups, you can draw meaningful conclusions about the differences in height between Group A and Group B. For example, you might find that the men in Group A are, on average, taller than the women in Group B, but that there is more variation in height within Group A than within Group B.
For example, suppose you have a sample of test scores for a class of students, and the mean score is 75 with a standard deviation of 10. If a student scored 85 on the test, you can calculate their z-score as follows:
z = (85 - 75) / 10 = 1
This means that the student's score is one standard deviation above the mean score for the class.
The z-score is an important concept in statistics because it allows you to compare data points from different populations or samples on a common scale. It also helps you identify outliers and extreme values in your data set.
For example, suppose you have two data sets with different means and standard deviations. Without standardizing the data, it would be difficult to compare the two sets directly. However, by calculating the z-scores for each data point, you can compare them on a common scale and make meaningful comparisons. Let's no look at an example to illustrate how z-scores can be used to compare two data sets with different means and standard deviations.
Imagine we need to compare the heights of Group A and Group B. Group A consists of 50 men with a mean height of 70 inches and a standard deviation of 3 inches. Group B consists of 50 women with a mean height of 64 inches and a standard deviation of 2.5 inches.
If you were to compare the raw data without standardizing it, it would be difficult to draw any meaningful conclusions. The heights of the men in Group A would be much higher than the heights of the women in Group B, simply because men are typically taller than women. However, by calculating the z-scores for each data point, you can compare the heights on a common scale and make meaningful comparisons.
To calculate the z-score for each data point, you would use the formula:
z = (x - μ) / σ
For Group A, the z-score for each data point would be:
z = (x - 70) / 3
For example, if a man in Group A is 73 inches tall, his z-score would be:
z = (73 - 70) / 3 = 1
For Group B, the z-score for each data point would be:
z = (x - 64) / 2.5
For example, if a woman in Group B is 66 inches tall, her z-score would be:
z = (66 - 64) / 2.5 = 0.8
By calculating the z-scores for each data point, you can compare the heights of the two groups on a common scale. A z-score of 1 in Group A represents a height that is one standard deviation above the mean for that group, while a z-score of 0.8 in Group B represents a height that is 0.8 standard deviations above the mean for that group.
You can also compare the distributions of the two groups by looking at the z-score distributions. The z-score distribution for Group A would have a mean of 0 and a standard deviation of 1, while the z-score distribution for Group B would have a mean of 0 and a standard deviation of 1. In other words, the z-scores for both groups are on the same scale and can be compared directly.
By comparing the z-scores for each data point and the z-score distributions of the two groups, you can draw meaningful conclusions about the differences in height between Group A and Group B. For example, you might find that the men in Group A are, on average, taller than the women in Group B, but that there is more variation in height within Group A than within Group B.
Z Score for Probabilities and Confidence Intervals
In addition to calculating z-scores for individual data points, you can also use the z-score to calculate probabilities and confidence intervals.
For example, the area under the normal distribution curve between -1 and 1 standard deviations from the mean is approximately 68%, meaning that about 68% of the data falls within this range. The area between -2 and 2 standard deviations from the mean is approximately 95%, and the area between -3 and 3 standard deviations from the mean is approximately 99.7%.
You can use these probabilities to calculate confidence intervals for your data set. For example, if you have a sample mean of 75 with a standard deviation of 10, you can calculate a 95% confidence interval as follows:
This means that you can be 95% confident that the true population mean falls between 71.08 and 78.92.
In conclusion, the z-score is a powerful tool in statistics that allows you to standardize data, compare data from different populations, and calculate probabilities and confidence intervals. By understanding how to calculate and interpret z-scores, you can gain deeper insights into your data and make more informed decisions.
For example, the area under the normal distribution curve between -1 and 1 standard deviations from the mean is approximately 68%, meaning that about 68% of the data falls within this range. The area between -2 and 2 standard deviations from the mean is approximately 95%, and the area between -3 and 3 standard deviations from the mean is approximately 99.7%.
You can use these probabilities to calculate confidence intervals for your data set. For example, if you have a sample mean of 75 with a standard deviation of 10, you can calculate a 95% confidence interval as follows:
- Calculate the standard error of the mean: SE = σ / sqrt(n) = 10 / sqrt(25) = 2
- Calculate the margin of error: ME = 1.96 * SE = 1.96 * 2 = 3.92
- Calculate the lower and upper bounds of the confidence interval: 75 - 3.92 = 71.08 and 75 + 3.92 = 78.92
This means that you can be 95% confident that the true population mean falls between 71.08 and 78.92.
In conclusion, the z-score is a powerful tool in statistics that allows you to standardize data, compare data from different populations, and calculate probabilities and confidence intervals. By understanding how to calculate and interpret z-scores, you can gain deeper insights into your data and make more informed decisions.
You can use this z score probability calculator to calculate right and left tail probabilities given a positive or a negative z score:
Z-Score Calculator Probability Calculator
Enter z-score:
Enter probability level:
Left tail probability:
Right tail probability: