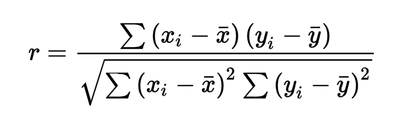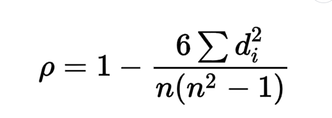Understanding the Correlation Coefficient: A Comprehensive Guide
Statistical analysis is an essential component of many fields, from finance to psychology to sociology, among others. One of the most common techniques used in statistics is measuring the relationship between two variables - a process facilitated by the correlation coefficient. This comprehensive guide will explain the concept of the correlation coefficient, provide examples, and detail how to interpret its value.
What is the Correlation Coefficient?
The correlation coefficient is a statistical measure that calculates the strength of the relationship between the relative movements of two variables. The values range between -1.0 and 1.0. A calculated number greater than 1.0 or less than -1.0 means that there was an error in the correlation measurement.
A correlation of -1.0 shows a perfect negative correlation, while a correlation of 1.0 shows a perfect positive correlation. A correlation of 0.0 shows no linear relationship between the movement of the two variables.
A correlation of -1.0 shows a perfect negative correlation, while a correlation of 1.0 shows a perfect positive correlation. A correlation of 0.0 shows no linear relationship between the movement of the two variables.
Types of Correlation Coefficients
There are several types of correlation coefficients, but the most commonly used are Pearson's correlation coefficient (r) and Spearman's rank correlation coefficient.
Pearson's Correlation Coefficient
Pearson's correlation coefficient, also known as Pearson's r, is a statistical measure that quantifies the strength and direction of a linear relationship between two variables. It's most appropriate to use when both variables are normally distributed and have a linear relationship.
The formula for Pearson's r is:
r = Σ[(xi - x̄)(yi - ȳ)] / √[Σ(xi - x̄)² * Σ(yi - ȳ)²]
Pearson's Correlation Coefficient
Pearson's correlation coefficient, also known as Pearson's r, is a statistical measure that quantifies the strength and direction of a linear relationship between two variables. It's most appropriate to use when both variables are normally distributed and have a linear relationship.
The formula for Pearson's r is:
r = Σ[(xi - x̄)(yi - ȳ)] / √[Σ(xi - x̄)² * Σ(yi - ȳ)²]
Where:
• xi and yi are the individual sample points indexed with i
• x̄ is the mean (average) of the x values
• ȳ is the mean of the y values
• Σ denotes the sum of the values indicated
Spearman's Rank Correlation Coefficient
Spearman's rank correlation coefficient, or Spearman's rho, is a non-parametric measure of the strength and direction of association that exists between two ranked variables. It's most appropriate when one or both variables are ordinal or when they're not normally distributed.
The formula for Spearman's rho is:
ρ = 1 - [(6 * Σdi²) / (n * (n² - 1))]
Where:
• di is the difference between the ranks of corresponding variables
• n is the number of observations
• Σ denotes the sum of the values indicated
Correlation Coefficient Examples
Let's illustrate the concept of the correlation coefficient with two examples.
Example 1: Pearson's Correlation Coefficient
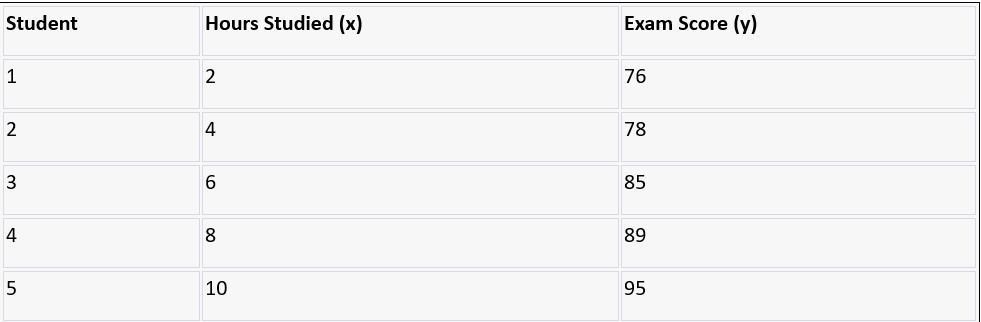
Consider a researcher investigating a potential correlation between time spent studying for an exam and the score achieved on the exam.
Here's the data for 5 students:
Example 1: Pearson's Correlation Coefficient
Consider a researcher investigating a potential correlation between time spent studying for an exam and the score achieved on the exam.
Here's the data for 5 students:
The first step is to find the sums and squares of the x and y values and the sum of the products of x and y:
Σx = 2 + 4 + 6 + 8 + 10 = 30
Σy = 76 + 78 + 85 + 89 + 95 = 423
Σx² = 2² + 4² + 6² + 8² + 10² = 220
Σy² = 76² + 78² + 85² + 89² + 95² = 36161
Σxy = 276 + 478 + 685 + 889 + 10*95 = 2470
Now plug these values into the formula for Pearson's r:
r = [5 * Σxy - Σx * Σy] / sqrt{ [5 * Σx² - (Σx)²] * [5 * Σy² - (Σy)²] }
r = [5 * 2470 - 30 * 423] / sqrt{ [5 * 220 - 30²] * [5 * 36161 - 423²] }
r = 0.989 // Approximate value, indicating a strong positive correlation
This strong positive correlation suggests that more hours spent studying is associated with higher exam scores.
Example 2: Spearman's Rank Correlation Coefficient
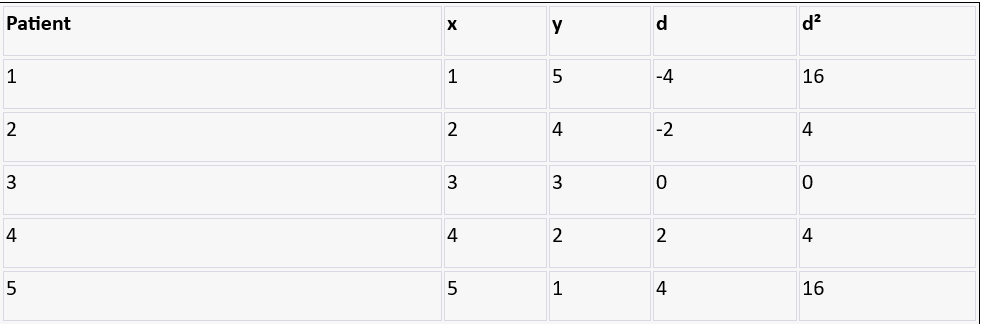
Consider a clinical researcher investigating a potential correlation between the rank of a patient's pain severity (on a scale of 1 to 5) and the rank of the improvement reported after a new treatment.
Here's the data for 5 patients:
Σx = 2 + 4 + 6 + 8 + 10 = 30
Σy = 76 + 78 + 85 + 89 + 95 = 423
Σx² = 2² + 4² + 6² + 8² + 10² = 220
Σy² = 76² + 78² + 85² + 89² + 95² = 36161
Σxy = 276 + 478 + 685 + 889 + 10*95 = 2470
Now plug these values into the formula for Pearson's r:
r = [5 * Σxy - Σx * Σy] / sqrt{ [5 * Σx² - (Σx)²] * [5 * Σy² - (Σy)²] }
r = [5 * 2470 - 30 * 423] / sqrt{ [5 * 220 - 30²] * [5 * 36161 - 423²] }
r = 0.989 // Approximate value, indicating a strong positive correlation
This strong positive correlation suggests that more hours spent studying is associated with higher exam scores.
Example 2: Spearman's Rank Correlation Coefficient
Consider a clinical researcher investigating a potential correlation between the rank of a patient's pain severity (on a scale of 1 to 5) and the rank of the improvement reported after a new treatment.
Here's the data for 5 patients:
The first step is to find the differences between the ranks (d) and then square these differences (d²):
d = x - y
d² = d²
d = x - y
d² = d²
Now, plug these values into the Spearman's rank correlation coefficient formula:
ρ = 1 - [ (6 * Σd²) / (n³ - n) ]
ρ = 1 - [ (6 * 40) / (5³ - 5) ]
ρ = -1
A correlation coefficient of -1 implies a perfect negative correlation, suggesting that patients with more severe pain reported greater improvement after the treatment.
ρ = 1 - [ (6 * Σd²) / (n³ - n) ]
ρ = 1 - [ (6 * 40) / (5³ - 5) ]
ρ = -1
A correlation coefficient of -1 implies a perfect negative correlation, suggesting that patients with more severe pain reported greater improvement after the treatment.
Interpreting the Correlation Coefficient
Interpreting the correlation coefficient involves understanding its magnitude (strength) and direction.
Strength
The closer the correlation coefficient is to 1 or -1, the stronger the correlation. A coefficient of 0.8, for example, indicates a strong positive relationship, while a coefficient of -0.8 indicates a strong negative relationship. Conversely, a coefficient close to 0 indicates no linear relationship.
Direction
The sign of the correlation coefficient indicates the direction of the relationship. A positive coefficient indicates a positive correlation — as one variable increases, the other also increases. A negative coefficient, on the other hand, denotes a negative correlation — as one variable increases, the other decreases.
Strength
The closer the correlation coefficient is to 1 or -1, the stronger the correlation. A coefficient of 0.8, for example, indicates a strong positive relationship, while a coefficient of -0.8 indicates a strong negative relationship. Conversely, a coefficient close to 0 indicates no linear relationship.
Direction
The sign of the correlation coefficient indicates the direction of the relationship. A positive coefficient indicates a positive correlation — as one variable increases, the other also increases. A negative coefficient, on the other hand, denotes a negative correlation — as one variable increases, the other decreases.
Use Cases of Correlation Coefficients
Correlation coefficients are used in a variety of fields to measure how certain variables are interdependent.
- In finance, it can be used to compare the performance of a stock or investment portfolio with the market or other stocks and portfolios.
- In psychology, it can measure the relationship between variables like stress and health conditions.
- In medicine, it can analyze the correlation between different treatments and patient outcomes.
- In sociology, it can evaluate the link between social factors like education level and income.
Correlation Coefficients and the z-score
In statistics, the z-score is another crucial concept that plays a vital role in understanding the correlation coefficient. It's a measure of how many standard deviations a data point is from the mean. The z-score can be calculated for each value in a dataset, and then a correlation coefficient can be calculated for the z-scores.
If a dataset is transformed into z-scores and the correlation coefficient is calculated for the transformed dataset, the result will be the same as if the correlation coefficient was calculated for the original dataset. This property is useful in many statistical tests that assume normally distributed data, as transforming to z-scores can help meet this assumption.
The correlation coefficient is an essential concept in statistics, which allows us to understand and quantify the relationship between two variables. Through the examples and detailed explanations provided in this guide, you should now have a more in-depth understanding of the correlation coefficient and how to interpret it effectively.
If a dataset is transformed into z-scores and the correlation coefficient is calculated for the transformed dataset, the result will be the same as if the correlation coefficient was calculated for the original dataset. This property is useful in many statistical tests that assume normally distributed data, as transforming to z-scores can help meet this assumption.
The correlation coefficient is an essential concept in statistics, which allows us to understand and quantify the relationship between two variables. Through the examples and detailed explanations provided in this guide, you should now have a more in-depth understanding of the correlation coefficient and how to interpret it effectively.