Normal vs Non-Normal Distribution: Understanding the Differences
Statistical analysis is a potent technique to comprehend and explain data. One important concept to understand is the difference between normal and non-normal distributions. In this blog post, we will discuss what normal and non-normal distributions are, the characteristics of each, and the implications for statistical analysis.
Normal Distribution
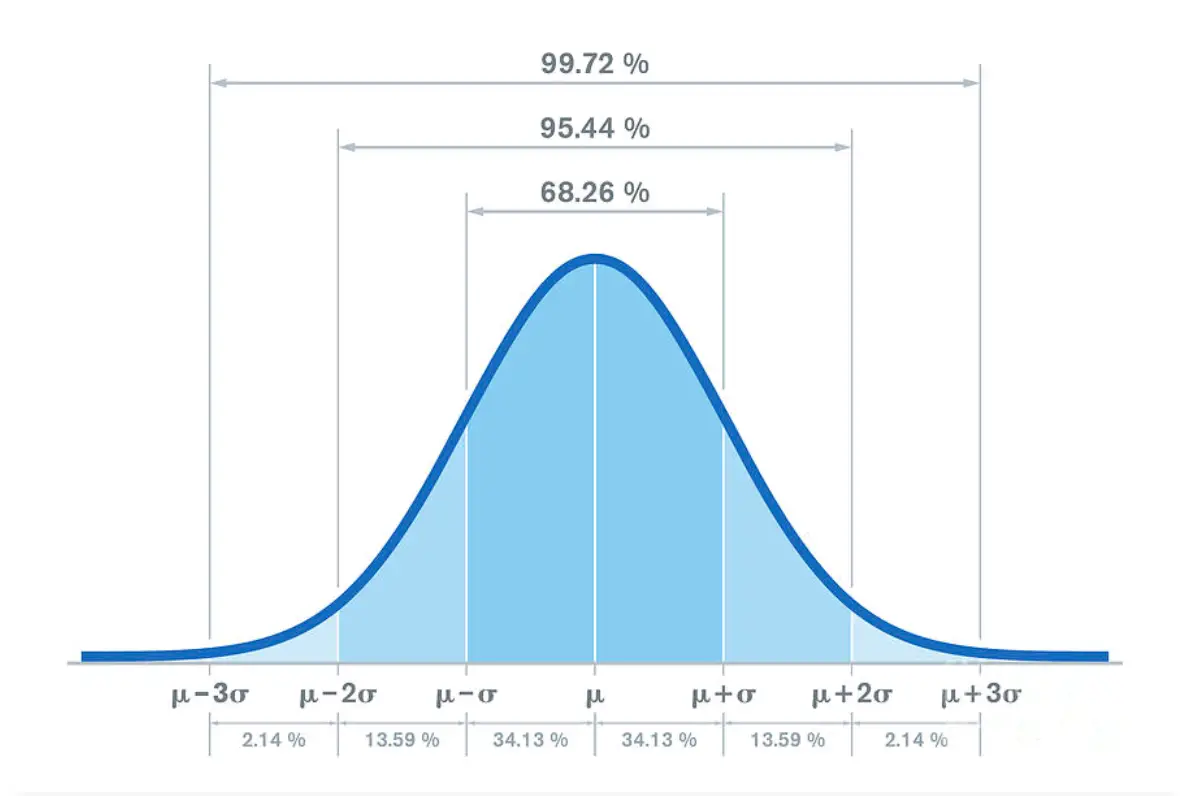
A bell-shaped curve that is symmetrically centered around the mean is called a normal distribution or Gaussian distribution. In a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations.
Some common examples of normal distributions include height and weight measurements, test scores, and IQ scores. Normal distributions are useful because they allow us to make predictions about the likelihood of a particular value occurring within a certain range.
Non-Normal Distribution
A non-normal distribution, on the other hand, is any distribution that does not follow a normal distribution. These distributions can take many different shapes, including skewed, bimodal, and uniform.
Some common examples of non-normal distributions include income, stock prices, and the number of daily visitors to a website. Non-normal distributions can be more challenging to analyze than normal distributions because they do not have the same predictable patterns.
Implications for Statistical Analysis
The choice of statistical test depends on the distribution of the data. When the data follows a normal distribution, parametric tests such as the t-test and ANOVA can be used. However, when the data is non-normal, non-parametric tests such as the Wilcoxon rank-sum test and the Kruskal-Wallis test may be more appropriate.
It is important to note that some statistical tests are robust to violations of normality assumptions, meaning they can still be used even if the data is not perfectly normal. However, it is always best to check the distribution of the data before selecting a statistical test.
Understanding the difference between normal and non-normal distributions is essential for accurate statistical analysis. Knowing the characteristics of each type of distribution and the appropriate statistical tests to use can help ensure that data is properly analyzed and interpreted.
It is important to note that some statistical tests are robust to violations of normality assumptions, meaning they can still be used even if the data is not perfectly normal. However, it is always best to check the distribution of the data before selecting a statistical test.
Understanding the difference between normal and non-normal distributions is essential for accurate statistical analysis. Knowing the characteristics of each type of distribution and the appropriate statistical tests to use can help ensure that data is properly analyzed and interpreted.
FAQs: Normal vs Non-Normal Distribution
Q: What is a normal distribution?
A: A normal distribution, also known as a Gaussian distribution, is a statistical distribution that is symmetrical around the mean. In a normal distribution, most data points are clustered around the mean, with fewer points at the tails. The shape of a normal distribution is a bell curve.
Q: What is a non-normal distribution?
A: A non-normal distribution is any statistical distribution that is not normal. Non-normal distributions can take many different shapes, including skewed, bimodal, and uniform. Non-normal distributions are more challenging to analyze than normal distributions because they do not have the same predictable patterns.
Q: What are some examples of normal distributions?
A: Some common examples of normal distributions include height and weight measurements, test scores, and IQ scores. In general, any measurement that is the result of the sum of many independent random variables tends to follow a normal distribution.
Q: What are some examples of non-normal distributions?
A: Some common examples of non-normal distributions include income, stock prices, and the number of daily visitors to a website. Non-normal distributions can be more challenging to analyze because they do not have the same predictable patterns as normal distributions.
Q: Why is it important to know whether data is normally distributed?
A: It is important to know whether data is normally distributed because the choice of statistical test depends on the distribution of the data. When the data follows a normal distribution, parametric tests such as the t-test and ANOVA can be used. However, when the data is non-normal, non-parametric tests such as the Wilcoxon rank-sum test and the Kruskal-Wallis test may be more appropriate.
Q: Can non-normal data be transformed into a normal distribution?
A: Yes, non-normal data can be transformed into a normal distribution using mathematical transformations such as logarithms or square roots. However, it is important to note that transforming data can change the interpretation of the results and may not always be appropriate.
Q: What are some common methods for testing normality?
A: There are several methods for testing normality, including the Shapiro-Wilk test, the Anderson-Darling test, and the Kolmogorov-Smirnov test. These tests compare the distribution of the data to a normal distribution and determine whether the data is significantly different.
Q: What should I do if my data is not normally distributed?
A: If your data is not normally distributed, you should consider using non-parametric tests such as the Wilcoxon rank-sum test and the Kruskal-Wallis test. These tests are more robust to violations of normality assumptions and can be used when the data is not perfectly normal.
Q: What are some common mistakes people make when analyzing non-normal data?
A: One common mistake people make when analyzing non-normal data is assuming that the data is normally distributed and using parametric tests such as the t-test or ANOVA. Another mistake is transforming the data without considering the implications of the transformation on the interpretation of the results.
A: A normal distribution, also known as a Gaussian distribution, is a statistical distribution that is symmetrical around the mean. In a normal distribution, most data points are clustered around the mean, with fewer points at the tails. The shape of a normal distribution is a bell curve.
Q: What is a non-normal distribution?
A: A non-normal distribution is any statistical distribution that is not normal. Non-normal distributions can take many different shapes, including skewed, bimodal, and uniform. Non-normal distributions are more challenging to analyze than normal distributions because they do not have the same predictable patterns.
Q: What are some examples of normal distributions?
A: Some common examples of normal distributions include height and weight measurements, test scores, and IQ scores. In general, any measurement that is the result of the sum of many independent random variables tends to follow a normal distribution.
Q: What are some examples of non-normal distributions?
A: Some common examples of non-normal distributions include income, stock prices, and the number of daily visitors to a website. Non-normal distributions can be more challenging to analyze because they do not have the same predictable patterns as normal distributions.
Q: Why is it important to know whether data is normally distributed?
A: It is important to know whether data is normally distributed because the choice of statistical test depends on the distribution of the data. When the data follows a normal distribution, parametric tests such as the t-test and ANOVA can be used. However, when the data is non-normal, non-parametric tests such as the Wilcoxon rank-sum test and the Kruskal-Wallis test may be more appropriate.
Q: Can non-normal data be transformed into a normal distribution?
A: Yes, non-normal data can be transformed into a normal distribution using mathematical transformations such as logarithms or square roots. However, it is important to note that transforming data can change the interpretation of the results and may not always be appropriate.
Q: What are some common methods for testing normality?
A: There are several methods for testing normality, including the Shapiro-Wilk test, the Anderson-Darling test, and the Kolmogorov-Smirnov test. These tests compare the distribution of the data to a normal distribution and determine whether the data is significantly different.
Q: What should I do if my data is not normally distributed?
A: If your data is not normally distributed, you should consider using non-parametric tests such as the Wilcoxon rank-sum test and the Kruskal-Wallis test. These tests are more robust to violations of normality assumptions and can be used when the data is not perfectly normal.
Q: What are some common mistakes people make when analyzing non-normal data?
A: One common mistake people make when analyzing non-normal data is assuming that the data is normally distributed and using parametric tests such as the t-test or ANOVA. Another mistake is transforming the data without considering the implications of the transformation on the interpretation of the results.