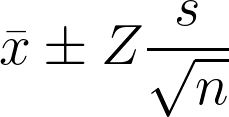Confidence Interval Calculator
This user-friendly tool is designed to help you calculate the confidence interval for a given set of data. Whether you are a student, a statistician, or a researcher, you'll find this tool handy and time-saving.
Just input your sample mean, population standard deviation, sample size, and choose your desired level of confidence. With a single click on "Calculate," the tool calculates the confidence interval, lower and upper bounds, margin of error, and standard error.
Just input your sample mean, population standard deviation, sample size, and choose your desired level of confidence. With a single click on "Calculate," the tool calculates the confidence interval, lower and upper bounds, margin of error, and standard error.
How to Use the Confidence Interval Calculator
- Input the Sample Mean: This value represents the average of the collected sample data. It is calculated by adding up all the values in the dataset and then dividing by the number of values in that dataset.
- Input the Population Standard Deviation: This value represents how spread out the population data are from the mean. In other words, it gives a measure of the variability of the population data. If this value is not known, an estimate from a sample can be used.
- Input the Sample Size: This is the number of observations that make up the sample. It is represented as 'n'. Note that a larger sample size will typically give a more accurate representation of the population parameter.
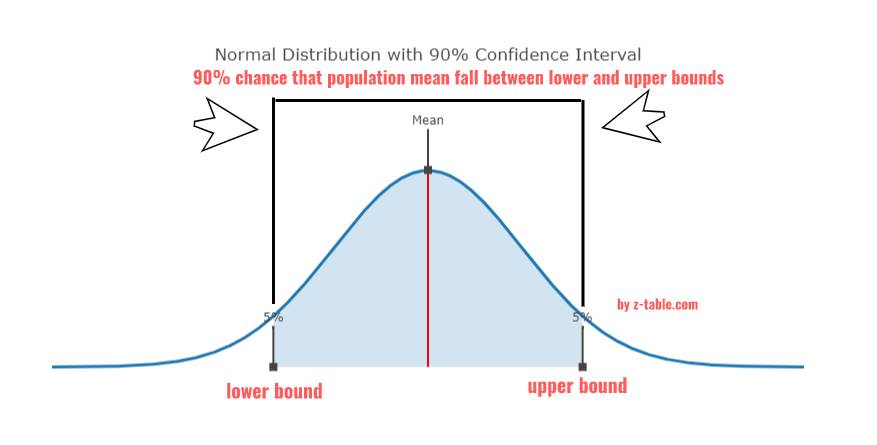
- Select the Confidence Level: The confidence level gives the probability that the population parameter lies within the calculated confidence interval. It is expressed as a percentage. For example, a 95% confidence level means that we can be 95% confident that the population parameter lies within the calculated confidence interval.
- Click 'Calculate': After filling in all of the above information, click on the 'Calculate' button.
Understanding the Confidence Interval Calculator Output
- Confidence Interval: This range estimate is where the population parameter (mean) lies with the given level of confidence. It is expressed in the format: sample mean ± margin of error.
- Margin of Error: This value provides the range of potential values above and below the sample mean. It is calculated using the z-value, standard deviation, and sample size.
- Lower Bound & Upper Bound: These values provide the range of the confidence interval. The lower bound is calculated by subtracting the margin of error from the sample mean. The upper bound is calculated by adding the margin of error to the sample mean.
- Standard Error: The standard error reflects the standard deviation of the sample mean's distribution. It is calculated as the standard deviation divided by the square root of the sample size. Please note, a larger sample size will generally produce a narrower confidence interval, since it more accurately represents the population. Similarly, a higher confidence level will produce a wider confidence interval, as it covers more potential values for the population parameter.
- Z-Score: The Z-Score represents the critical value that corresponds to the desired confidence level. It indicates how many standard deviations an element is from the mean. A positive Z-Score implies that the element is above the mean, while a negative Z-Score implies that the element is below the mean. The Z-Score is an important factor in determining the appropriate margin of error and, consequently, the width of the confidence interval.
How to Calculate Confidence Interval
A confidence interval is a range of values that likely contains an unknown population parameter. It is widely used in statistics for hypothesis testing and estimating population parameters. A confidence interval is an indication of your measurement's reliability and is always given with a confidence level, often 95% or 99%.
Understanding Confidence Intervals
Let's use an example. Suppose you have been tasked to estimate the average height of men in your city. It would be time-consuming and practically impossible to measure the height of every man. Hence, you select a random sample of men, measure their heights, and calculate the average height. But how confident are you that this average height represents the actual average height of all men in your city?
This is where a confidence interval comes into play. A 95% confidence interval for this example might be 170 cm ± 10 cm. This means you can be 95% confident that the average height of all men in your city lies between 160 cm and 180 cm.
Now, the width of the confidence interval depends on several factors, including the standard deviation of the sample, the sample size, and the confidence level. Let's break it down:
This is where a confidence interval comes into play. A 95% confidence interval for this example might be 170 cm ± 10 cm. This means you can be 95% confident that the average height of all men in your city lies between 160 cm and 180 cm.
Now, the width of the confidence interval depends on several factors, including the standard deviation of the sample, the sample size, and the confidence level. Let's break it down:
Confidence Level and Z-score
A key component of confidence intervals is the concept of the Z-score. The Z-score is a measure of how many standard deviations an element is from the mean. In the context of confidence intervals, we use the Z-score to define our desired confidence level.
For a 95% confidence level, the Z-score is approximately 1.96. This means that if your data is normally distributed, about 95% of values are within 1.96 standard deviations of the mean. Similarly, for a 99% confidence level, the Z-score is approximately 2.576. Hence, the larger the Z-score, the larger your confidence interval will be.
For a 95% confidence level, the Z-score is approximately 1.96. This means that if your data is normally distributed, about 95% of values are within 1.96 standard deviations of the mean. Similarly, for a 99% confidence level, the Z-score is approximately 2.576. Hence, the larger the Z-score, the larger your confidence interval will be.
Calculating Confidence Intervals
Now let's delve into the calculation part. There are four main steps to compute a confidence interval:
- Identify a sample statistic: Since we are trying to estimate a population mean, we choose the sample mean (x̄) as the sample statistic.
- Select a confidence level: In this analysis, the confidence level is defined for us in the problem. We are working with a 95% confidence level.
- Find the standard deviation or standard error: Depending on what information you have available, you will either find the standard deviation (σ) or standard error (SE). Remember, standard error is the standard deviation of the sample mean's distribution, which can be calculated by dividing the standard deviation by the square root of the sample size.
- Compute the margin of error (MOE): Elsewhere on this site, we show how to compute margin of error when the sampling distribution is approximately normal. The key steps are shown below:
- Find standard deviation or standard error.
- Multiply by the appropriate Z-score (depending on your selected confidence level).
- For a 95% confidence level, use a Z-score of 1.96. For a 99% confidence level, use a Z-score of 2.576.
- Compute the Confidence Interval (CI): The range of the confidence interval is defined by the formula:
x̄ ± Z*(σ/√n)
Confidence Interval Calculation Example
Suppose we have a sample size (n) of 500 people. The sample mean (x̄) height is 170 cm, and the population standard deviation (σ) is 15 cm. We want to calculate a 95% confidence interval for the population mean height.
- Our sample mean (x̄) is 170 cm.
- Our confidence level is 95%, so our Z-score is 1.96.
- The standard deviation (σ) is 15 cm, so the standard error (SE) will be 15/√500 ≈ 0.67 cm.
- The margin of error (MOE) is ZSE, which is 1.960.67 ≈ 1.31 cm.
- Hence, the 95% confidence interval (CI) is 170 ± 1.31, or from 168.69 cm to 171.31 cm.