Variability Definition in Statistics: Understanding Variability and Its Importance in Data Analysis4/29/2023 Statistics is a part of mathematics that focuses on the collection, analysis, interpretation, and presentation of numbers. One of the fundamental concepts in statistics is variability, which refers to the degree of spread or dispersion of a set of data. In this post, we will explore the variability definition in statistics and its importance in data analysis. What is Variability in Statistics?Variability, also known as dispersion, is a measure of how spread out a set of data is. It refers to the differences or variations that exist among the values in a data set. Variability can be observed in various statistical measures, such as range, variance, standard deviation, and coefficient of variation. The concept of variability is essential in statistics because it provides valuable information about the characteristics of the data set. For example, a data set with high variability indicates that the values are widely spread out and may have extreme values, while a data set with low variability indicates that the values are closely clustered around the mean or average. Measures of Variability in StatisticsAs mentioned earlier, variability can be measured using different statistical measures. Let's discuss some of these measures: Range The range is the difference between the highest and lowest values in a data set. It is a simple measure of variability that describes how dispersed the data is. However, it has limitations as it only considers the two extreme values and does not provide information about the distribution of the data. Variance Variance is a measure of how far the data is spread out from its mean. It is calculated by taking the sum of the squared deviations of each data point from the mean and dividing it by the total number of observations minus one. The formula for variance is: Variance = Σ (xi - μ)2 / (n - 1) Where Σ is the sum, xi is the data value, μ is the mean, and n is the sample size. The variance is useful in identifying how much variation exists in the data set. A high variance indicates that the data points are far away from the mean, while a low variance indicates that the data points are close to the mean. Standard Deviation Standard deviation is the square root of variance. It is a widely used measure of variability that provides information about the dispersion of the data points around the mean. The formula for standard deviation is: Standard Deviation = √(Σ (xi - μ)2 / (n - 1)) The standard deviation is often used in statistics because it is easy to interpret and has useful properties, such as the empirical rule. Coefficient of Variation The coefficient of variation is a measure of relative variability that is useful when comparing data sets with different means and units. It is calculated by dividing the standard deviation by the mean and multiplying the result by 100. The formula for the coefficient of variation is: Coefficient of Variation = (Standard Deviation / Mean) x 100 The coefficient of variation provides a way of comparing the degree of variability between data sets of different scales. Importance of Variability in Data AnalysisVariability is an essential concept in data analysis as it provides valuable insights into the nature of the data set. Here are some of the reasons why variability is important in data analysis:
Identifying Outliers Outliers are data points that lie far away from the other values in the data set. Variability measures, such as standard deviation and variance, can help identify outliers by indicating the degree of spread or dispersion in the data. Making Inferences Variability measures are essential in making statistical inferences about the population based on sample data. The variability measures, such as standard deviation, variance, and coefficient of variation, provide information about how closely the sample data represents the population. A low variability indicates that the sample data is more representative of the population, while a high variability indicates that the sample data may not be representative. Evaluating Data Quality Variability measures are useful in evaluating the quality of data. A high variability may indicate errors in data collection or measurement, while a low variability may indicate a lack of diversity or insufficient sample size. Monitoring Process Stability Variability measures are often used in process control to monitor the stability of a process. A stable process is one that produces consistent results with low variability, while an unstable process produces inconsistent results with high variability. Comparing Data Sets Variability measures, such as the coefficient of variation, are useful in comparing data sets with different means and units. The coefficient of variation provides a standardized measure of variability that can be used to compare the degree of variation between data sets. To summarize, variability is a fundamental concept in statistics that refers to the degree of spread or dispersion of a set of data. Variability measures, such as range, variance, standard deviation, and coefficient of variation, provide valuable information about the characteristics of the data set. Variability is important in data analysis as it helps identify outliers, make inferences, evaluate data quality, monitor process stability, and compare data sets. By understanding variability, we can gain a deeper insight into the nature of the data and make more informed decisions based on the data analysis.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Z Score Table BlogEverything about normal distribution and Z scores Archives
January 2024
Categories |
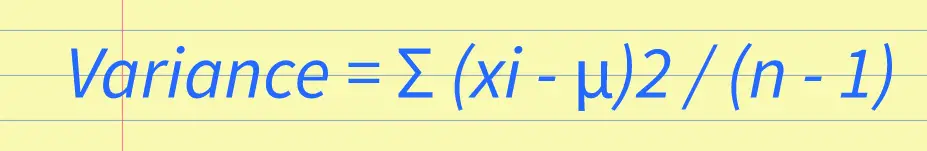
 RSS Feed
RSS Feed